CORRELATIONS
SPECIFICATION: Correlations. Analysis of the relationship between co-variables. The difference between correlations and experiment
Correlation is made of Co- (meaning "together") and Relationship.
Correlation means relationship - more precisely, it measures the extent to which two variables are related.
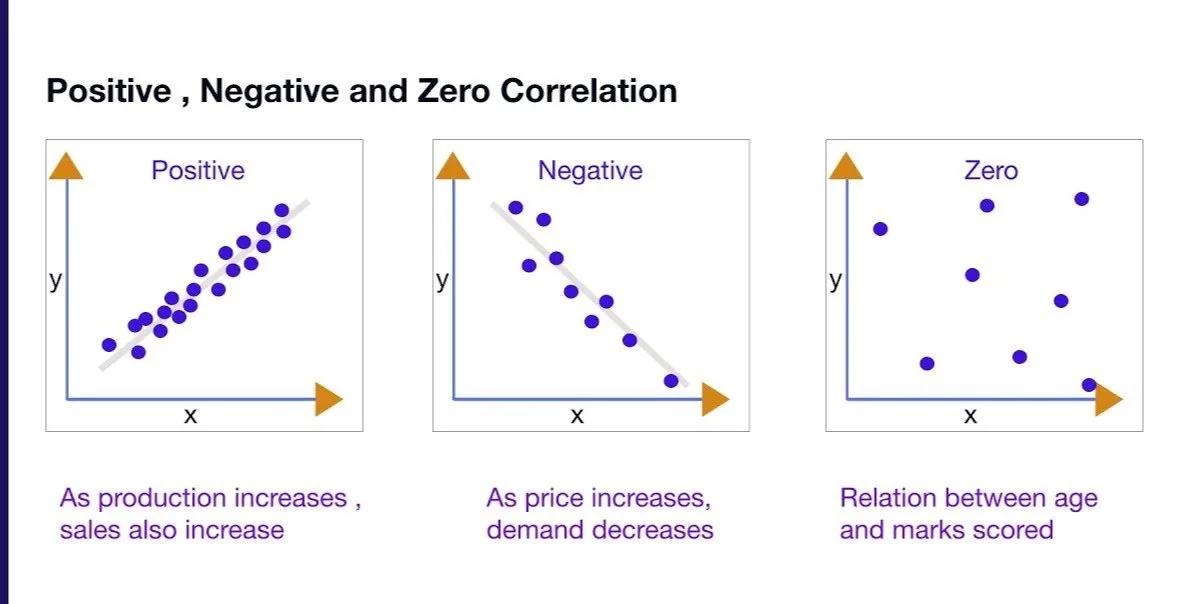
Correlation is the descriptive statistical technique measuring the relationship between two variables. Literally, these techniques measure co-relationships between variables - the extent to which values on one variable are associated with high values on another variable. If an increase in one variable is associated with an increase in the other variable, this is known as a positive correlation. An example would be height and weight. As people get taller, they tend to get heavier.
If an increase in one variable is associated with a decrease in the other, this is known as a negative correlation. An example would be height above sea level and temperature: As you climb the mountain (increase in height), it gets colder (decrease in temperature).
When there is no relationship between two variables, this is known as a zero correlation. For example, there is no relationship between the amount of tea drunk and the level of intelligence.
Strictly speaking, correlation is not a research method but a way of analysing data gathered by other means. This might be useful, for example, if we wanted to know if there was a relationship between watching violence on T.V. and a tendency towards violent behaviour in adolescence because it is I’m, possible to test this hypothesis experimentally.
Another area where correlation is widely used is in the study of intelligence. Research has been carried out to test the strength of the association between the I.Q. levels of identical and non-identical twins.
CORRELATION COEFFICIENTS
Correlations calculate a coefficient which tests the strength of the correlation. In short, the coefficient is an inferential statistic that objectively calculates the relationship between two variables. For example, if you asked me the correlation between stress and illness, I could say, “quite strong, but my answer is subjective and therefore unmeasurable. With coefficients, the numbers calculated describe the links between two variables completely.
The correlation coefficient (r) indicates the extent to which the pairs of numbers for these two variables lie in a straight line. Values over zero indicate a positive correlation, while values under zero indicate a negative correlation.
+1 known as a perfect positive correlation
-1 known as a perfect negative correlation
0 known as zero (no) correlation
The strength of the correlation (i.e. the degree of the relationship) increases as a calculated correlation coefficient moves away from zero and becomes closer to either +1 or -1. Correlation coefficients
Instead of drawing a scattergram, a correlation can be expressed numerically as a coefficient,
When working with ordinal data, the correlation coefficient to use is Spearman’s rho
When working with interval data, the correlation coefficient is Pearson’s r.
DIFFERENCES BETWEEN CORRELATIONS AND EXPERIMENTS
INTERESTING CORRELATIONS ABOUT BREAD
More than 98% of convicted criminals are bread eaters.
50% of all children who grow up in bread-consuming households score below average on standardised tests.
More than 90% of violent crimes are committed within 24 hours of eating bread.
Primitive tribal societies that have no bread exhibit a low occurrence of cancer, Alzheimer’s disease, Parkinson's disease, and osteoporosis.
Bread has been proven to be addictive as people deprived of bread and given only water to eat beg for bread within 24 hours.
Bread is often a "gateway" food item, leading users to "harder" items such as butter, jam, marmite, peanut butter and even chocolate spread.
Newborn babies can choke on bread.
In the 18th century, when virtually all bread was baked in the home:
The average life expectancy was less than 50 years
Infant mortality rates were unacceptably high
Many women died in childbirth
Diseases such as typhoid, yellow fever and influenza ravaged whole nations.
Correlations can show a link or relationship between variables, but as you can see from the above examples, these links may be meaningless and have no cause-and-effect connection.
An experiment isolates and manipulates the independent variable to observe its effect on the dependent variable and controls the environment so that extraneous variables may be eliminated. Experiments establish cause and effect. A correlation identifies variables and looks for a relationship between them. An experiment tests the effect that an independent variable has upon a dependent variable, but a correlation looks for a relationship between two variables. This means that the experiment can predict cause and effect (causation). Still, a correlation can only predict a relationship, as another extraneous variable that is not known about may be involved.
TYPES OF CORRELATIONS
POSITIVE CORRELATION ++ is the most common; as one variable increases, so does the other, e.g., IQ and GCSE score in the example above.
NEGATIVE CORRELATION - -: as one variable increases, the other decreases, e.g. it might be fair to assume that the higher your stress levels, the lower your life expectancy. Again, we are unable to show cause and effect. As mentioned frequently in ‘Stress,’ illnesses could be due to secondary habits such as smoking, poor diet, etc. Please note that the minus sign before negative correlations does not denote negative numbers,
ZERO (NO) CORRELATION
DIRECTIONAL (1-TAILED) & NON-DIRECTIONAL (2-TAILED) HYPOTHESES
Both positive and negative correlations are directional hypotheses or 1-tailed hypotheses. This is because, in both cases, they are predicting a direction.
When a researcher is unsure if the results will be positive or negative and so predicts any correlation instead, this is an example of a non-directional or 2-tailed hypothesis. This is because the researcher is not predicting a direction.
Let’s take the following example to illustrate this point:
Research has shown that intelligence between siblings is positively correlated, probably because either IQ is inherited or siblings experience similar education.
A psycho-dynamic psychologist disputes the findings of such correlations as he believes intelligence and birth order are negatively correlated between siblings, e.g., older siblings are more intelligent than younger siblings. He believes that this is because older children are given more responsibility than younger children. Moreover, older children have never recovered from being usurped by younger siblings, so they aim to please their parents (this might translate to doing well at school).
The psychodynamic psychologist opts for a non-directional hypothesis because previous research has shown a positive correlation and not a negative one.
EXAMPLES:
DIRECTIONAL (1-TAILED HYPOTHESES) There will be a positive correlation between IQ and birth order
DIRECTIONAL (1-TAILED HYPOTHESES) There will be a negative correlation between IQ and birth order
NON-DIRECTIONAL (2-TAILED HYPOTHESES) There will be a correlation between IQ and birth order
Null hypothesis: There will be no correlation between IQ and birth order
GRAPHS AND CORRELATION COEFFICIENTS
Correlations are best illustrated using scattergrams/scattergraphs. When you draw a scattergram, it doesn't matter which variable goes on the x-axis and which goes on the y-axis. Remember, in correlations, we are always dealing with paired scores, so the values of the two variables taken together will be used to make the diagram. Decide which variable goes on each axis and then put a cross at the point where the two values coincide.
A perfect positive correlation has a coefficient of + 1.0; no correlation has a coefficient of 0. In the real world, neither of these extremes usually exists. Coefficients lie somewhere between 0 and +1.0 for positive correlations and between 0 and -1.0 for negative—the nearer 1.0, the higher the correlation. The board expects you to be able to guess a correlation coefficient.
Below, I’ve included a few examples:
Amount of r Strength of correlation
0.0 < 0.1 no correlation
0.1 < 0.3 little correlation
0.3 < 0.5 medium correlation
0.5 < 0.7 high correlation
0.7 < 1very high correlation
POSITIVE OR NEGATIVE CORRELATIONS?
Positive correlations are two variables travelling in the same direction, either:
Increasing together ++
Decreasing together - -
Negative correlations are two variables travelling in different directions.
As one variable increases +
The other variable decreases -
Zero correlations are variables travelling in random directions and forming no pattern.
CORRELATION OR QUASI EXPERIMENT?
"Female participants aged 15-24 will exercise more than female participants aged 25-34."
"Older men will excercise less than younger men."
IDENTIFYING THE RESEARCH METHOD NEEDED FOR EACH STUDY:
The first hypothesis suggests comparing different age groups rather than directly examining the relationship between age and exercise This scenario is better suited for a quasi-experimental design, where age is treated as a categorical variable rather than a continuous one.
The second hypothesis implies a correlation analysis where age is treated as a continuous variable.
Distinguishing the Research Method:
While both hypotheses involve age, the distinction lies in how age is treated in the analysis. For instance, if age is defined as discrete categories, a quasi-experimental design would be more appropriate. On the other hand, if age is considered a continuous variable, then a correlation analysis would be more suitable.
Quasi-experiments typically involve three variables: the independent variable (e.g., age groups such as those aged 15-24 and those aged 25-34), the dependent variable (e.g., smoking behavior), and potentially a third variable. The age groups are treated as the independent variable, and smoking behavior serves as the dependent variable. Therefore, this aligns with a quasi-experimental design.
On the other hand, correlation designs typically involve examining the relationship between two continuous variables. When age is defined as a continuous variable (e.g., with no discrete categories such as age 15-24 or 25-34), it meets the criteria for a correlation analysis. As a general rule, correlations involve two variables, while quasi-experimental designs involve a minimum of three.
INTERCLASS AND INTRACLASS CORRELATIONS , CONCORDANCE-RATES, INTER-RATER-RELIABILITY & INTER-CLASS-CORRELATIONS
Many correlations have both sets of data coming from the same person.
For example: “There will be a positive correlation between a smoker’s age and the number of cigarettes smoked; the older the person, the more cigarettes they will smoke.”
In this example, both age and the number of cigarettes smoked come from one person.
However, interclass and intra-class correlation are two cases of correlation analysis where the comparison is between groups.
“Interclass” means among the groups.
“Intra class” (also similar to concordance rates and inter-rater-reliability) means within the group
What is the difference between interclass and intraclass correlation?
Interclass correlation shows the association among the groups, and intra-class correlation shows the association within a group. In statistics, the interclass correlation (or interclass correlation coefficient) measures a relation between two variables of different classes (types), such as the weights of 20-year-old daughters and the weights of their 50-year-old mothers. The Pearson correlation coefficient is the most commonly used measure of interclass correlation.
The interclass correlation contrasts with the intraclass correlation between variables of the same class, such as the weights of women and their identical twins; here, deviations are measured from the mean of all members of the single class: in this example, of all women in the set of identical twins.
Although many psychology courses do not ask students to distinguish between these different types of correlations, they expect students to learn about concordance rates and inter-rater reliability, so explaining the differences makes sense. I have found students become confused with between-quasi-designs and intraclass correlations (concordance rates) otherwise.
Here is another way of putting it
An intraclass correlation (ICC) is a statistical method used to assess the degree of agreement or similarity among observations made on the same subjects, groups, or clusters. It measures the consistency or reliability of measurements made within the same group.
For example, consider a study comparing the IQ scores of older siblings and younger siblings within the same families. In this scenario, each family represents a cluster, and the IQ scores of siblings within each family are compared. The ICC would assess the extent to which IQ scores within the same family are similar or correlated.
The confusion between ICC and quasi-experimental designs arises because both involve comparing groups of related individuals. However, the key distinction lies in the nature of the relationship between participants.
In quasi-experimental designs, participants are typically unrelated individuals assigned to different groups or conditions based on pre-existing characteristics or criteria. For example, comparing the IQ scores of individuals from different age groups or educational backgrounds would constitute a quasi-experimental design.
On the other hand, in ICC studies, participants are related or clustered in some way, such as family members, students within the same classroom, or patients within the same healthcare facility. The focus is on examining the agreement or similarity of measurements within these related groups.
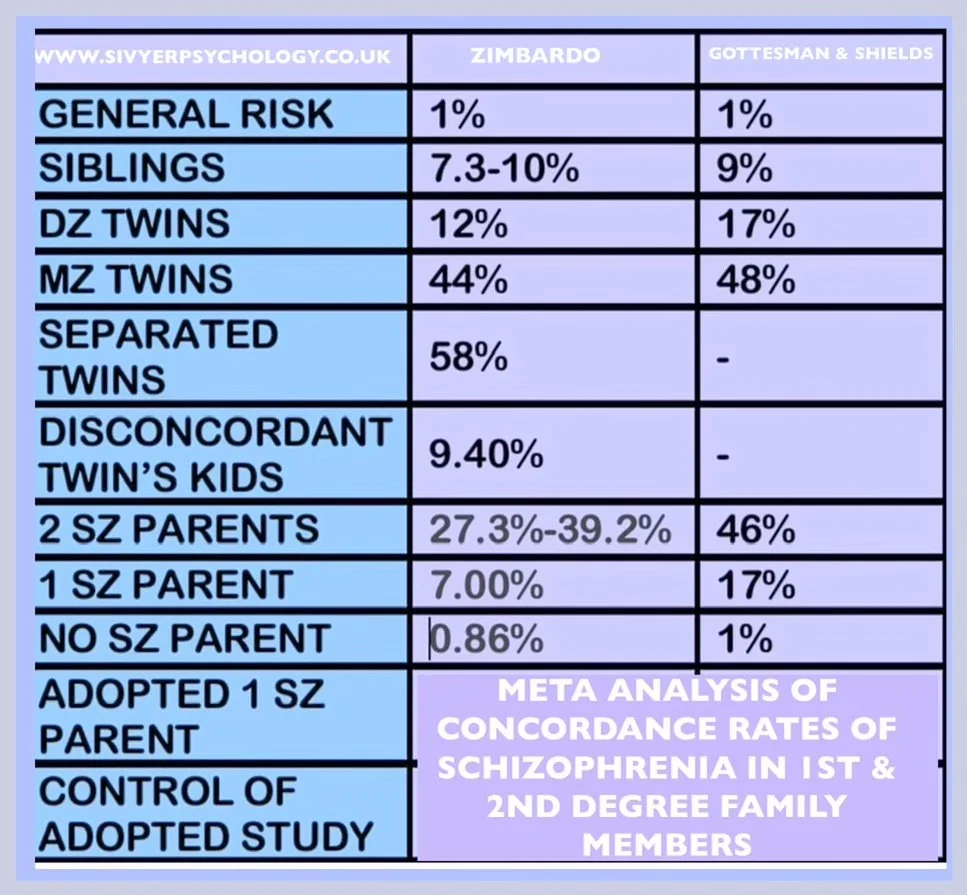
Intraclass correlations (ICCs) are often used to assess the degree of agreement or similarity among observations made on related individuals or groups. Concordance rates of schizophrenia within families are an excellent example of ICCs in practice.
In this context, researchers might investigate the prevalence of schizophrenia among family members, such as parents, siblings, and children of individuals diagnosed with schizophrenia. The ICC would measure the extent to which the occurrence of schizophrenia is consistent or correlated within these family units.
In summary, while both ICC studies and quasi-experimental designs involve comparing groups of individuals, the distinction lies in whether the participants are related or clustered. ICC studies assess agreement within related groups, whereas quasi-experimental designs compare unrelated individuals across different groups or conditions
EXAMPLES OF INTRA-CLASS CORRELATIONS ARE CONCORDANCE RATES OF SCHIZOPHRENIA IN FAMILIES
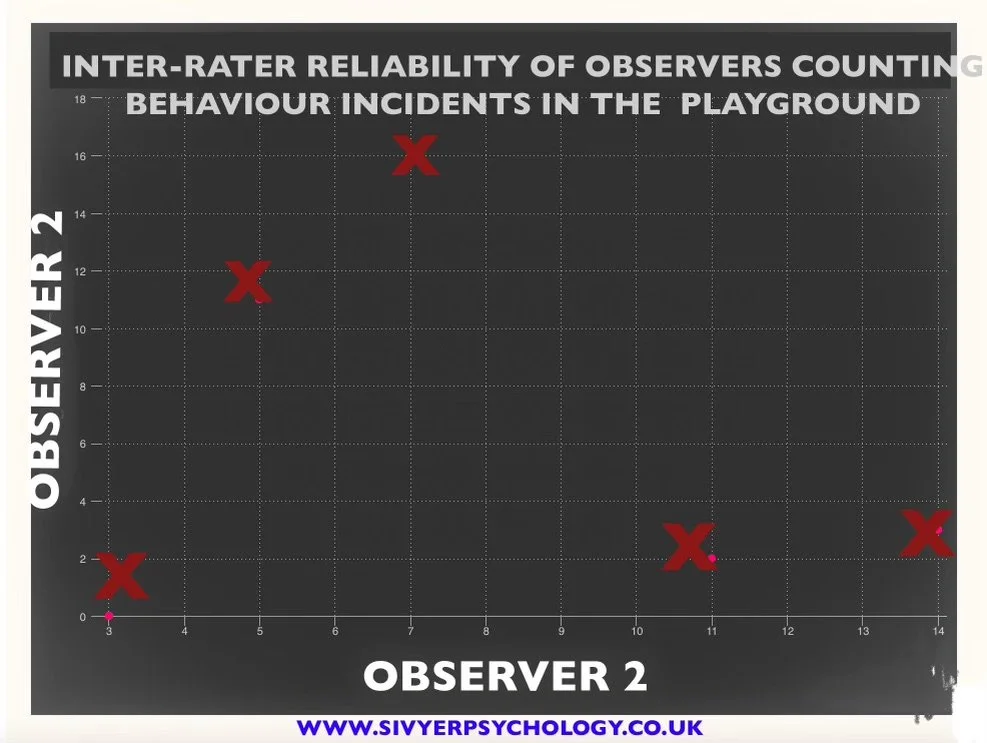
Inter-rater reliability refers to the consistency or agreement among different raters or observers when assessing the same set of data. Since the raters are not related to each other, it falls under the category of inter-class correlation rather than intra-class correlation.
STRENGTHS AND USES OF CORRELATIONS
Correlation allows the researcher to investigate naturally occurring variables that may be unethical or impractical to test experimentally. For example, it would be unethical to experiment on whether smoking causes lung cancer.
Correlation allows the researcher to see if there is a relationship between variables. This can then be displayed in a graphical form.
Correlation allows the researcher to conduct preliminary research: Before going to the expense and time involved in experimenting, a correlation can test the water to see if a relationship exists between variables.
Investigation: Researchers can make inferences about how one variable influences another when experimenting is either unethical or impossible.
Correlation allows the researcher to measure concordance rates between family members where one is mentally ill, for example.
Correlation allows the researcher to test for the reliability of measurements
• Test-retest reliability (are measures consistent).
• Inter-rater reliability (are observers consistent).
LIMITATIONS
Correlation does not and cannot be taken to imply causation. Even if two variables have a strong association, we cannot assume that one causes the other. For example, suppose we found a positive correlation between watching violence on TV and violent behaviour in adolescence. It could be that the cause of both these is a third (extraneous) variable - for example, growing up in a violent home - and that both the watching of T.V. and the violent behaviour are the outcome of this.
Correlation does not allow us to go beyond the data that is given. For example, suppose it was found that there was an association between time spent on homework (1/2 hour to 3 hours) and number of G.C.S.E. passes (1 to 6). It would not be legitimate to infer from this that spending 6 hours on homework would likely generate 12 G.C.S.E. passes.
Curvilinear correlations
Correlations don’t always lie in a straight line. For example, when we looked at the effects of anxiety on recall, we saw an inverted ‘U’ shaped correlation between low levels and high levels of anxiety, resulting in lower levels of recall (the Yerkes-Dodson law)
Beware of spurious correlations.
Sales of ice cream are closely correlated to drownings in swimming pools and the number of shark attacks! According to QI, in the UK, in the 20th century, hair length was closely correlated to performance on the Stock Market, as were lengths of women's skirts! There are no obvious causal factors in any of these; rather, third variables cause both. Even reputable broadcasters report what, at first glance, may appear to be bona fide relationships, such as the correlation between clumsiness in childhood and, later, adult obesity.
QUESTIONS
As a biker’s speed increases, their time to get to the finish line decreases.
As humidity increases, people's desire to be outside may decrease.
As snowfall totals increase, the number of people driving decreases.
As the slope of a hill increases, the speed a walker reaches may decrease.
As the temperature decreases, people purchase more heaters.
As the temperature increases, customers buy fewer hot chocolate products.
If it is darker outside, more light is needed inside.
If the temperatures outside decrease dramatically, heating bills will increase.
In areas with low amounts of rain, more wild animals migrate to other places.
As a tadpole gets older, its tail gets smaller.
The longer someone runs, the less energy they have.
The more one eats, the less hunger one will have.
The more one exercises, the fewer health problems they are likely to have.
The more one smokes cigarettes, the more one's ability to breathe deeply decreases.
The warmer it is outside, the fewer layers of clothing one has to wear to be warm.
A rosebush with many thorns will attract fewer animals who want to eat it.
A student who has many absences has a decrease in grades.
As a child grows, so does their clothing size.
As a student’s study time increases, so do their test averages.
As a tree gets more mature, it requires water less frequently.
As algae increases in a lake, a certain species of algae-eating fish increases.
As it snows more, the sales of snow shovels go up.
As one exercises more, their body weight decreases.
As one increases in age, often one's agility decreases.
As the amount of moisture increases in an environment, the growth of mould spores increases.
As the number of trees cut down increases, the probability of erosion increases.
As the percentage of salt in salty water increases, buoyancy increases.
As the speed of a wind turbine increases, the amount of electricity generated increases.
As the temperature decreases, the speed at which molecules move decreases.
As the temperature goes up, ice cream sales also go up.
As the wattage of light bulbs increases, the light output increases
As the weather gets colder, air conditioning costs decrease.
As tread on your car’s tyres decreases, traction with the road decreases.
As you drink more coffee, the number of hours you stay awake increases.
As you eat more antioxidants, your immune system improves.
Becoming more involved with school activities increases students' self-esteem.
When enrolment at college decreases, the number of teachers decreases.
Hiring more salespeople will result in the company making more sales.
If a car decreases speed, travel time to a destination increases.
If a car tyre has more air, the car may use less gas per mile.
If a train increases speed, the time to reach the final point decreases.
In archaeology, a more stable landform means more site visibility.
Investing in professional development for teachers also increases overall student achievement.
Schools with high test scores also have high graduation rates.
Students with strong attendance records also have higher grades.
The faster a jet pilot flies, the higher the G-forces are.
The larger a herd of animals gets, the less food there is.
The less time you spend marketing your business, the fewer new customers you will have.
The longer you spend in the bath, the more wrinkly your skin becomes.
The longer someone invests, the more compound interest they will earn.
The longer your hair grows, the more shampoo you will need.
The more customers spend in the economy, the higher a country's GDP (Gross Domestic Product).
The more gasoline you put in your car, the farther it can go.
The more money you save, the more financially secure you feel.
The more one works, the less free time one has.
The more time you spend running on a treadmill, the more calories you burn.
The more time you study or prepare for a test, the fewer mistakes you'll make.
The more years of education you complete, your earning potential will be higher.
The more you exercise your muscles, the stronger they get.
The more you pay off a loan, the less debt you'll have.
The older an animal gets, the fewer offspring it can have.
When an animal's hunger increases, its self-protection decreases.
When an employee works more hours, their paycheck also increases.
When employees make a high salary, efficiency increases.
When enrolment at college decreases, the number of teachers decreases.
When lions sleep more, they have less time to hunt during the day.
When the employment level is high, inflation rises due to increased economic money.
When the supply of a particular product decreases, the demand for it increases.
When workers get a raise, morale improves.
When you spend more time brushing your teeth, you'll have fewer cavities
Possible Exam Questions
1. A psychological study recorded the number of hours that children spent in a daycare setting from birth to three years old and asked each child’s primary caregiver to rate their child for aggression. The study found that, as the number of hours spent in day care increased, the parents’ aggression rating also increased. What type of correlation is this research indicating? (1 mark)
Exam Hint: Most students will be able to identify correctly that this is, in fact, a positive correlation because as one variable increases, so does the other.
2. Discuss why it might be more appropriate for a researcher to use a correlation study rather than an experiment. (3 marks)
Exam Hint: Answers that state that a correlational study looks for a relationship and experiments to investigate differences will only gain one mark here. To access further marks, students must be able to explain issues around manipulating variables and ethics.
3. Outline one strength and one weakness of using correlational methods in psychological research. (4 marks)
Exam Hint: Many students can consider the main weakness of correlations but struggle to outline a strength correctly. Strengths include studying the relationship between variables that occur naturally or measuring things that cannot be manipulated experimentally.