DISCREET AND CONTINUOUS DATA
DISCRETE AND CONTINUOUS DATA
In simpler terms, discrete data is like counting marbles—you end up with whole, countable numbers. Continuous data is more like pouring sugar; you can have a very precise amount (down to the grain), and it can vary by very small fractions
DISCRETE AND CONTINUOUS DATA
Discrete and categorical data are subsets of quantitative data.
Data can either be discrete or continuous.
In general, variables (and data) represent measurements on some continuous scale or information about some categorical or discrete characteristics.
DISCREET OR CATEGORICAL DATA
Shoe sizes are a classic example of discrete data, because sizes 39 and 40 mean something, but size 39.2, for example, does not.. Discrete data usually occurs when there are only a certain number of values or when we count something (using whole numbers).
With discrete data, ambiguity does not exist; distinctions are clear-cut. For instance, gender is binary in this context; one cannot transition from male to female within the parameters of discrete data.
Occupation and marital status are examples of categorical or discrete variables. These variables sort individuals into distinct categories based on their status or role without implying any inherent order (for occupation) or with a clear, non-numerical categorisation (for marital status).
Marital Status: This variable categorises individuals based on their legal or social partnership status. The typical categories include "never married," "married," "divorced," "widowed," etc. Each category is distinct and mutually exclusive, meaning an individual can belong to only one category at a time.
Occupation: This categorises individuals based on their job or profession, such as "teacher," "engineer," "doctor," "unemployed," etc. While the categories can be numerous and varied, each represents a distinct type of employment or professional activity.
The respondents' weight, height, and age in a survey are classic examples of continuous data. This is because these measurements can vary in infinitely divisible ways within a range. A person's weight, height, or age can change over time and be recorded with great precision, such as 68.5 kilograms, 175.25 centimetres, or 29.75 years.
Graph 2 illustrates a set of discrete data characterised by the fact that the data points, in this case, dogs, represent countable units that cannot be subdivided. The nature of discrete data is such that there are no possible values between any two consecutive data points. In practical terms, you cannot have a fraction of a dog; there's a clear, unbridgeable gap between having one and two dogs. This quality of discreteness underscores the specific quantitative data where only whole, distinct counts are possible, making it perfectly suited for counting and enumeration tasks such as tallying the number of dogs.
NB: Notice the gaps between the graph variables showing discreet/cartographical data. The gaps represent where one variable ends and another begins. The variables do not continue into each other.
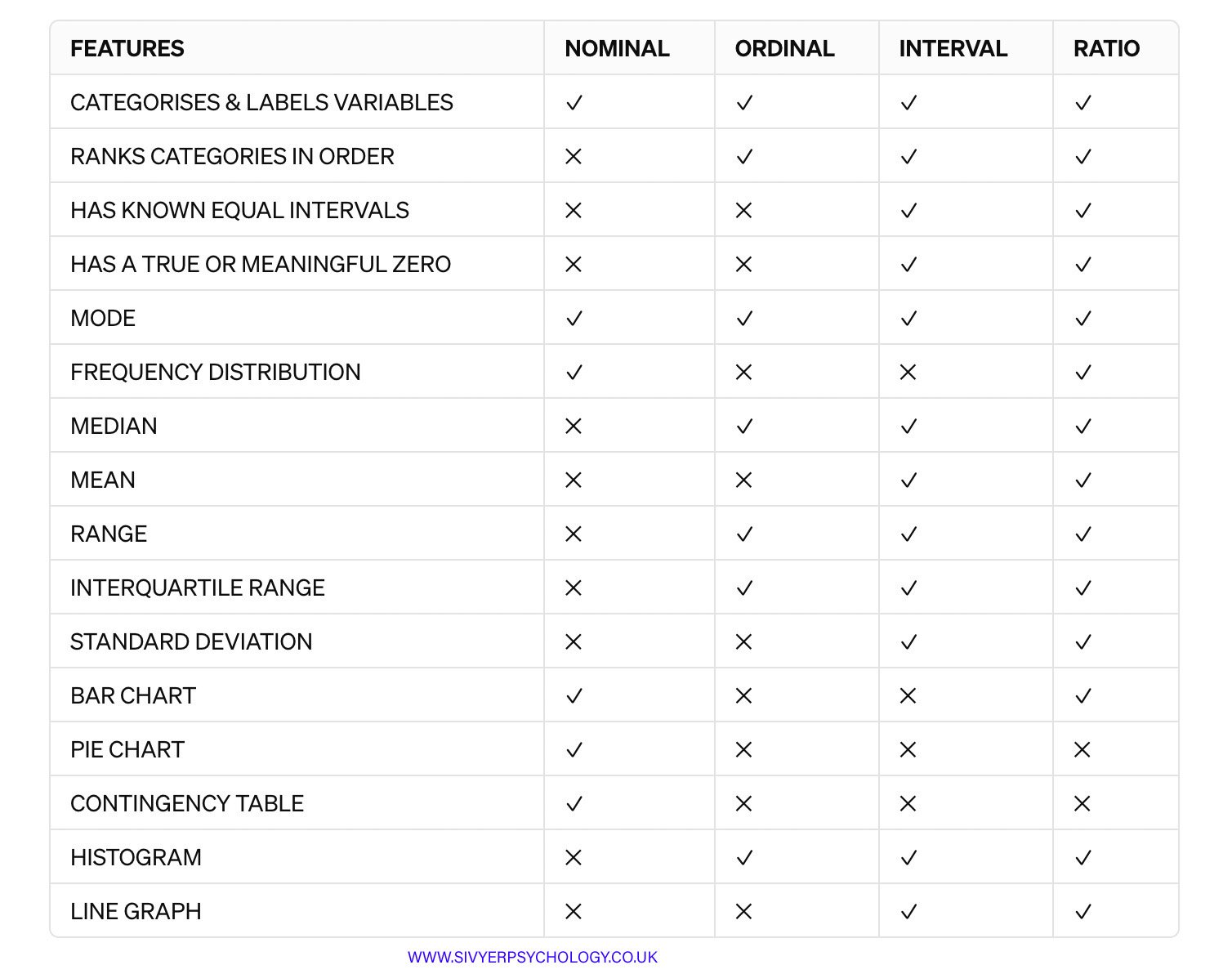
WHY CERTAIN MEASURES ARE SUITABLE FOR DISCRETE DATA
Discrete data, defined by its distinct and countable values, requires specific statistical measures to capture its characteristics accurately.
MODE FOR DISCRETE DATA
Direct Relevance: The mode representing the most frequently occurring value in a dataset directly aligns with the nature of discrete data. Since discrete data points are countable and distinct, identifying the mode provides a clear insight into the most prevalent category within the dataset. This is especially useful in cases where data points are non-numerical or when looking to identify the most common occurrence within categorical data, such as survey responses or demographic information.
MEDIAN FOR DISCRETE DATA
Applicability to Ordered Categories: The median is particularly relevant for ordinal discrete data, which, while discrete, maintains a logical order. Calculating the median—finding the middle value in a ranked list—offers a central tendency measure that remains unaffected by outliers. This is crucial in discrete datasets where extreme values can skew the average, but the median will still accurately reflect the central point of the distribution. It’s suitable for ordinal data where ranking matters, but the actual distance between ranks is not uniform or is irrelevant.
LIMITATIONS OF MEAN FOR DISCRETE DATA
While it's possible to calculate the mean for any set of numerical data, applying it to discrete data can be misleading and inappropriate. Discrete data is characterised by distinct, separate categories or specific, countable quantities, where each value carries a unique significance. Averaging these distinct categories or counts dilutes their meanings, leading to analyses that don't accurately reflect the nature of the data. For instance, when researching gender differences in dating ads across discrete categories such as status, appearance, personality, and hobbies, computing an average across these varied dimensions would not yield meaningful insights. Each category represents a separate aspect of the data and should be analyzed individually rather than amalgamated into a single mean value. Attempting to do so would result in an analysis that is not only statistically flawed but also conceptually nonsensical.
GRAPHICAL REPRESENTATIONS FOR DISCRETE DATA
The choice of bar charts and pie charts as graphical representations for discrete data reflects their ability to delineate between distinct categories or values, which is fundamental in conveying the characteristics of discrete datasets:
Bar Charts: Essential for discrete data as they visually separate each category with spaces between bars, emphasizing the distinct nature of each category or value. This makes it easy to compare frequencies or counts across different categories.
Pie Charts are effective for showing how categories within discrete data contribute to a whole, visually representing proportions or percentages. Each slice of the pie chart represents a distinct category, making it straightforward to understand the composition of the data at a glance.
In conclusion, mode and median are appropriate for discrete data analysis because they accurately reflect the most common occurrences and central points within datasets that consist of distinct, separate categories or values. Understanding these distinctions and applying the correct measures of central tendency and graphical representations are crucial in accurately interpreting discrete data.
EXAMPLES OF CATEGORICAL/DISCREET DATA
A five-question quiz is given in a Math class. The number of correct answers on a student's quiz is an example of discrete data. The number of correct answers would have to be one of the following: 0, 1, 2, 3, 4, or 5. There is no infinite number of values. Therefore, this data is discrete. In addition, if we were to draw a number line (axis) and place each possible value on it, we would see a space between each pair of values.
To obtain a taxi license in London, a person must pass a written exam regarding different locations in the city. How many times a person would take to pass this test is also an example of discrete data. A person could take it once, or twice, or 3 times, or 4 times, or…. Therefore, the possible values are 1, 2, and 3. There are infinitely many possible values, but if we put them on a number line (axis), we would see a space between each pair of values.
CONTINUOUS DATA
SEE GRAPH 3 FOR AN EXAMPLE OF A CONTINUOUS DATA GRAPH
Continuous data is a cornerstone of quantitative research, enabling a detailed and precise world exploration. Its ability to capture an extensive range of values with infinite precision makes it a fundamental tool in the arsenal of researchers across disciplines
Below is a breakdown of its defining characteristics:
SCALE OF MEASUREMENT Continuous data operates on a scale where each increment holds significance, no matter how minute. This attribute allows for measurements with near-limitless precision. Unlike discrete data, which is limited to specific, countable values, continuous data can reflect subtle variations within measurements, enhancing the accuracy of data representation.
RANGE OF VALUES The versatility of continuous data is evident in its capacity to cover any numeric value within a defined spectrum. This range may be finite or extend to infinity, accommodating various measurements. This characteristic underscores the adaptability of continuous data in capturing precise details across various contexts.
FRACTIONAL VALUES A hallmark of continuous data is its divisibility into infinitesimally small segments, including fractions and decimals. This divisibility facilitates highly accurate measurements, allowing researchers to delve into the minutiae of their subjects. Such precision is particularly valuable in fields demanding exactitude, such as engineering and physics.
STATISTICAL RANGE The statistical range of continuous data, indicating the span between its lowest and highest points, illuminates the data's variability. This range reveals the diversity within a dataset, offering insights into the breadth of phenomena under study.
APPLICATIONS AND EXAMPLES Continuous data finds relevance in many real-world applications, from the quantification of time and temperature to the measurement of age, height, and weight. Its capacity to accommodate even the smallest changes makes it indispensable for detailed analysis and precise measurement in disciplines like physics, engineering, and advanced mathematics.
GRAPHICAL REPRESENTATION Graphs depicting continuous data, such as line graphs and histograms, are marked by the absence of gaps between variables. This continuous flow mirrors the inherent nature of the data, emphasising its unbroken, fluid character. Unlike discrete data, which is represented with clear separations to denote distinct categories, continuous data is illustrated to reflect its seamless variability.
WHICH DESCRIPTIVE STATISTICS DO YOU USE FOR DISCREET DATA?
LEVELS OF MEASUREMENT: Continuous data is further sub-divided into Interval and ordinal
MEASURES OF CENTRAL TENDENCY:
Mean: Essential for continuous data as it integrates all data points, providing a comprehensive average that reflects the sum of all values divided by their count.
Median: The median, being the middle value that divides a dataset into two halves, is not affected by extreme values, making it a critical statistic for representing the central tendency of continuous data accurately.
MEASURES OF DISPERSION: Range and standard deviation
GRAPHS: Line graphs, histograms, scatter graphs (correlations only).
Line Graphs are crucial for depicting trends in continuous data over time. The continuous nature of the data means that line graphs, which connect data points with lines, accurately represent the seamless flow and changes in the data over a continuum without gaps between the variables.
Histograms: Mandatory for illustrating the distribution of continuous data. Unlike bar charts used for discrete data, histograms feature bars that touch each other, signifying the continuous nature of the data. Each bar represents an interval of values, and the height indicates the frequency of data within that interval, making histograms perfectly suited for showing how continuous data are distributed across different ranges.
For continuous data, selecting the mean and median as measures of central tendency, along with the standard deviation and range for dispersion, is compulsory due to their ability to capture the essential characteristics of continuity and variability. Similarly, line graphs and histograms are obligatory graphical representations, as they uniquely accommodate the seamless nature of continuous data, allowing for a precise and coherent visualisation of trends, distributions, and relationships within the data.
COMPARISON WITH DISCREET DATA
Number Line Representation: While continuous data can be represented on a number line where every point has significance, discrete data is limited to specific, distinct values that do not support the same level of divisibility or infinite variability.
Value Specificity: Discrete data is characterized by specific values with distinct meanings, with gaps between these values where no valid measurements exist. In contrast, continuous data allows for an unbroken series of values with no gaps.
EXAMPLES OF CONTINUOUS DATA
The height of trees at a nursery is an example of continuous data. Is it possible for a tree to be 76.2" tall? Sure. How about 76.29"? Yes. How about 76.2914563782"? Absolutely! The possibilities depend upon the accuracy of our measuring device.
One general way to tell if data is continuous is to ask yourself if the data can take on values that are fractions or decimals. If your answer is yes, this is usually continuous data.
The time it takes for a light bulb to burn out is an example of continuous data. Could it take 800 hours? How about 800.7? 800.7354? The answer to all 3 is yes.
PRIMARY AND SECONDARY DATA
When researching, you have to gather information and evidence from various sources.
Primary sources provide raw information and first-hand evidence. Examples include interview transcripts, statistical data, and works of art. A primary source gives you direct access to the subject of your research.
Secondary sources provide second-hand information and commentary from other researchers. Examples include journal articles, reviews, and academic books. A secondary source describes, interprets, or synthesises primary sources.
Primary sources are more credible as evidence, but good research uses both primary and secondary sources.
QUESTIONS ON PRIMARY AND SECONDARY DATA
Read the item and then answer the questions that follow.
In a study of social cognition, a researcher studied perspective-taking in children aged five years and nine years. An overall perspective-taking score was calculated based on answers to a questionnaire. A high score indicated good perspective-taking and a low score indicated poor perspective- The scores are shown in the table below.
TABLE 2
.
Explain why the table data is primary, not secondary data. 2 MARKS.
Explain one strength of primary data. 3 MARKS
A researcher wanted to investigate whether a relationship existed between locus of control and resistance to social influence. Before the investigation began, he devised a questionnaire to measure locus of control.
Why would the researcher’s questionnaire produce primary data? 2 MARKS
Suggest one limitation of primary data. 2 MARKS
A psychologist is investigating the causes of addiction to gambling. She interviews people attending debt counselling for problem gamblers. She asks them to describe their family and early childhood, recording everything they say. She also looks at information in the gamblers’ debt counsellor reports.
Referring to this investigation, explain the difference between primary and secondary data. 4 MARKS
Please explain how the psychologist could continue her investigation by conducting a thematic analysis of the interview recordings. 6 MARKS.